Astrophysics question

[EternalFrustration]

I'm trying to develop a fictional quintuple star system, vaguely inspired by Xi Scorpii. Stars A and B revolve around each other, Star C revolves around the AB barycenter. Stars D and E revolve around each other. The ABC group and the DE group then revolve around each other.
My question is: how do I calculate the orbital periods? I've found several websites that will let you plug in values in Kepler's Third Law and spit out your remaining variable, but they all seem to be geared toward a planet orbiting a sun, or a moon orbiting a planet.
Could any of you please point me in the right direction of how to figure it out? I've seen the brilliant (and frankly a little bit scary) minds at work here, and I figure if anyone can help me out, chances are good they're here.
Thank you,
P

[cjameshuff]

http://en.wikipedia.org/wiki/Orbital_period#Two_bodies_orbiting_each_other

Treat the pairs and larger groups as single masses at their barycenter to get something close, provided their spacing is a small fraction of the distance from the third body. However, with realistic distances, it seems likely the ABC and DE groups will orbit at such a distance that their period is unlikely to be relevant. Even the period of an AB close-binary pair and moderately-close C seems likely to be on the order of centuries. (Alpha Centauri A and B take about 80 years, Proxima takes hundreds of thousands of years to orbit the two if it's actually gravitationally bound to them at all.)

[Bob B.]

The orbital period of two stars is given by the equation,



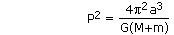
where P is the period, a is the semimajor axis (the distance between the stars), G is the constant of gravitation, and M and m are the masses of the two stars.

To get the period of C, I suppose you would just treat AB as a single mass located at the barycenter, with the semimajor axis being the distance between C and the AB barycenter.  Proceed similarly for the ABC and DE period.

In such a large system as this the periods would undoubtedly be effected by perturbations from the different stars, but in your case I'd ignore that.  Calculating each period as a simple two-body problem would probably be close enough.

[Chew]

You can substitute Solar masses and Astronomical Units in the equation to get the period in Earth years if you don't want to work with meters, kg, and seconds.

For instance, if the AB system has 1.5 solar masses and they are .5 AU apart they will orbit each other in (.5³ ÷ 1.5)^.5 = 0.2887 Earth years or 105.4 Earth days.

If the C star has 2 solar masses and is 10 AU from the AB system then the period will be (10³ ÷ (1.5 + 2 solar masses))^.5 = 16.9 Earth years.

If you want to have something orbiting one of these systems then beware the Hill sphere.