You make the same mistake as the rest of their comrades in astrophotography these tricks with the focus not work, you can not make the planet that is in the background looks larger than the one in the foreground
Tarkus, I had some time, so here's some data for you. I collated some easily located data on planetary distances and apparent size. The first two columns contain data on the perihelion and aphelion for each planet in the solar system. The next two show the minimum and maximum separation between each planet and Earth, calculated by simple addition or subtraction of the perihelion and aphelion data. Then we have data on the apparent sizes of the planets when observed from Earth. Finally, the columns in red show the ratio between maximum and minimum separation and maximum and minimum apparent size.
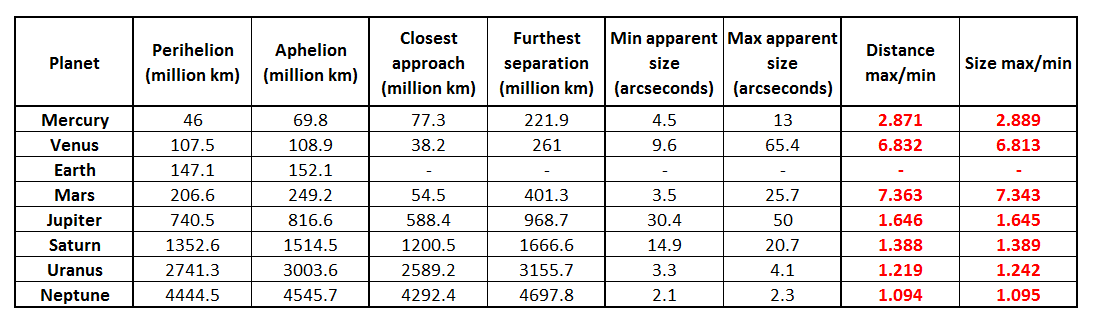
Firstly the data on the apparent sizes of the planets when viewed from Earth contradicts your statement that you can't have a planet in the background looking bigger than one in the foreground when astronomical distances are concerned. You'll notice, for example, that Mars always appears smaller than Jupiter despite being significantly closer to Earth at all times, that Venus does appear larger than Jupiter when at closest approach but appears significantly smaller when at maximum separation from Earth even though it is still 'in the foreground', and Mercury, the closest of all, always appears smaller than Jupiter
and Saturn. This, by the way, is something I and several others have personally verified by looking at these planets through telescopes with our own eyes: it is not a result of playing with photographic equipment.
Question 1: Given this, do you still maintain it is impossible for an object in the background to appear larger than one in the foreground?Secondly, the numbers in red show a clear relationship between distance and apparent size. For example, Venus is nearly seven times closer at closest approach and it appears 7 times larger. This relationship is the same, and the range over which it applies shows it is linear. In other words, if you get twice as close, something will appear twice as large, and if you get twice as far away, something will appear half the size. This relationship also clearly applies at astronomical distances, as here it is derived from astronomical observations of the planets that anyone can make with their own eyes and a telescope.
Question 2: Given this, and that Earth appears to be 2 degrees wide from 400,000km away, how big will it appear from twice as far away, at 800,000km?Two simple questions. Will you provide two simple answers? If not, why not?
[Edited to correct an error in the first question that is neatly captured by the quoted version later on...]